¿Te gusta el café? Quizás te interese conocer la física de la cafetera “estándar”. Concetto Gianino, “Experimental analysis of the Italian coffee pot “moka”,” American Journal of Physics, 75: 43-47, 2007, presenta la termodinámica de la cafetera mostrando que, aunque es termodinámicamente muy ineficiente como máquina de calor, no importa, ya que lo que realmente queremos es que el café resultante tenga un buen sabor. El artículo, desafortunadamente, no nos aclara cuándo se obtiene un café ideal (en cuanto a sabor).
¿Cómo es el café espresso ideal? Ernesto Illy, “The complexity of coffee,” Scientific American, 286: 8691, 2002, presenta un estudio de la química del café recién hecho y muestra que los sabores que se consideran más agradables se obtienen cuando la temperatura del agua es del orden de 93ºC, la presión es suficiente para permitir que el volumen de agua que atraviese el “cazo” de café granulado de la cafetera “moka” corresponda a una sola taza (entre 30 y 50 mililitros) y el agua fluya a través de éste durante unos 30 segundos o menos. Si el agua está más caliente de 95ºC, el café tiende a saber “quemado”, y si es menor que 93ºC, algunos de los sabores “más gustosos” del café se quedan en el grano.
¿Cómo podemos obtener un café ideal en una cafetera “estándar”? Warren D. King, “The physics of a stove-top espresso machine,” American Journal of Physics, 76: 558-565, June 2008, presenta un análisis de la cafetera estándar (exactamente la que aparece en la foto; por cierto, yo tengo una igual) con objeto de determinar la cantidad de agua con la que hay que rellenarla para obtener un café a la temperatura óptima (en el rango de 90 a 95 ºC).
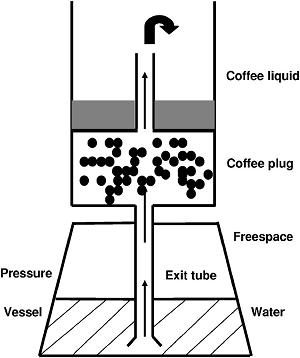
El funcionamiento de la cafetera es bien conocido. Se llena parcialmente de agua la vasija (vessel) a presión y se pone al fuego. El agua caliente se eleva por el tubo (exit tube) hasta alcanzar el contenedor con el café (coffee plug). Mezclada con el café el agua caliente sale por la parte superior en forma de café líquido. Este proceso puede durar varios minutos. El agua fluye hasta que el nivel de agua dismuye hasta que su nivel cae por debajo del tubo (exit tube). En este momento sólo vapor de agua puede ascender hacia arriba, produciendo el conocido “pitido,” señal sonora que nos advierte que el café está listo para ser servido.
¿Hay que esperar a que el agua hierva? No, aunque la mayoría de los manuales afirman que sí y que la presión dentro de la vasija tiene que ser la presión de vapor del agua. Esto no es necesario. De hecho, se puede obtener un café de mejor calidad si no permitimos que el agua llegue a hervir, eso sí, siempre y cuando no nos importe dejar de escuchar un sonoro ”pitido”.
Por supuesto, si calentamos la cafetera hasta una temperatura inferior a 100ºC el volumen de agua que se asciende como café puede ser inferior al volumen de la vasija. Si queremos un café mejor habrá que desaprovechar cierta cantidad de agua. Lo ideal es que el café se “cocine” a una temperatura inferior a 95ºC, aunque superior a 90ºC.
El artículo de Warren D. King presenta un modelo muy fácil de entender para la física de la cafetera que el propio autor valida utilizando datos experimentales de propia cosecha. Los experimentos son fáciles de repetir y pueden ser un buen objeto de estudio práctico para un laboratorio de física o de termodinámica.
Muchos dicen que los italianos son los reyes del buen café. Si sabes italiano (o te atreves a leer algo escrito en italiano) el artículo A. Varlamov, G.Balestrino, “La fisica di un buon caffè,” será de tu interés.