Lev Davidovich Landau nació el 22 de enero de 1908 en Bakú (Azerbaijan). Su entorno familiar influyó en su vocación científica, pues su padre era ingeniero trabajando en la industria petrolífera y su madre investigadora en fisiología.
Richard P. Feynman (1918-1988)
Richard Feynman es de los personajes que no necesitan presentación. No sólo fue uno de los más brillantes físicos de la historia (premio Nobel de física en 1965, inventor de los diagramas que llevan su nombre, y visionario de la computación cuántica y la nanotecnología), sino también una de las personalidades más admirables del s. XX. Excéntrico, bromista, y sin ataduras a los convencionalismos, fue definido en una ocasión por Freeman Dyson como “mitad genio, mitad bufón“, frase que luego corrigió a “todo genio, todo bufón” (como botón de muestra, Feynman se quejaba de que mientras siempre que iba a algún sitio a tocar los bongos le presentaban como un gran físico, cuando iba a dar una conferencia sobre física nunca le presentaban como un gran artista de los bongos).
Su entusiasmo desbordante, y la pasión por la ciencia que emanaba, hacía que los estudiantes adoraran sus clases, y que éstas fuesen de las más concurridas. Muchas de estas lecciones magistrales están editadas en colecciones de audio, pero también es posible disfrutar de algunas de ellas en vídeo. Concretamente, les informo que hay 46 vídeos de unos 8 minutos cada uno disponibles en Google Video. Estos corresponden a 4 lecciones que Feynman impartió en la Universidad de Auckland, Nueva Zelanda, en 1979 dentro del Memorial Douglas Robb. Las lecciones son las siguientes:
- Electrodinámica cuántica (fragmentos 1-10)
- Respuesta a las cuestiones de Newton sobre la luz (fragmentos 1-12)
- Electrones y sus interacciones (fragmentos 1-12)
- Nuevas cuestiones sobre la luz (fragmentos 1-12)
Son muy recomendables incluso si no se dispone de la base para seguir las lecciones, ya que siempre es todo un espectáculo ver a Richard Feynman en acción.
El video muestra simulaciones informática del mecanismo molecular unido al ADN en las células vivas. La primera película ilustra cómo la molécula de ADN se pliega y se enrolla para constituir los cromosomas en una célula en proceso de división. La segunda muestra la replicación de la molécula de ADN con abertura de la doble hélice y copia de cada cordón para formar dos moléculas nuevas de ADN.
Las propiedades mecánicas de las moléculas y de los agregados de átomos son de una gran importancia en biología y en nanotecnología. El equipo del profesor Marszalek se concentra en el estudio de las deformaciones plásticas y elásticas de los nanofilamentos y de los biopolímeros como proteínas, polisacáridos y, en este caso, el ácido desoxirribonucleico o ADN.
Para comprender lo que han hecho, evoquemos algunas nociones de la estructura del AND. Como puede verse en el esquema inferior, el ADN está compuesto de dos cordones enrollados constituidos por la reproducción periódica de un conjunto de fosfato-azúcar (desoxirribosa). Sobre este esqueleto se encuentra montada una distribución aperiódica de moléculas llamadas bases nitrogenados, representadas por sus símbolos A, T, G, C por Adenina, Timina, Guanina y Citosina. El conjunto forma parte de las moléculas conocidas con el nombre de nucleótidos.
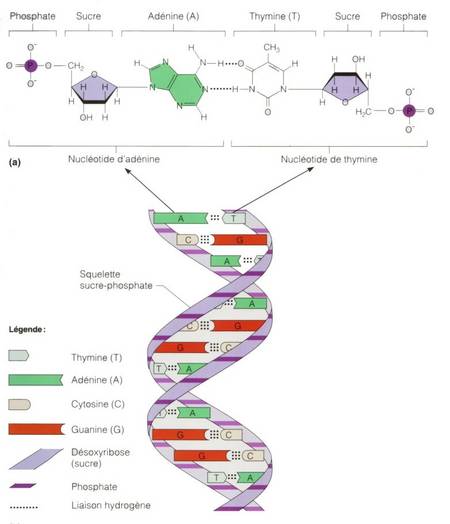 |
Para penetrar todos los secretos de los seres vivos, hay que comprender todas las propiedades fisicoquímicas de esta molécula. Pueden modelizarse algunas de ellas en biofísica gracias a la mecánica estadística de polímeros y a las ecuaciones de química cuántica. También se pueden hacer impresionantes simulaciones digitales del funcionamiento del ADN en las células. Sin embargo, toda teoría debe confrontarse con la realidad y, con harta frecuencia, los teóricos son incapaces de comprender los mecanismos y leyes que la naturaleza utiliza en realidad.
Una de las cuestiones importantes relativas al ADN es la de las fuerzas que estabilizan su estructura. En este caso se trata de comprender y modelizar los enlaces químicos entre bases complementarias y, finalmente, entre los agrupamientos fosfato-desoxirribosa y esas mismas bases nitrogenadas. Hasta ahora las características de esas fuerzas se habían deducido indirectamente a partir de mediciones hechas sobre BRINS de ADN no separadas y resultaba difícil aislar las contribuciones de las diferentes fuerzas.
Para orillar esta dificultad, los investigadores utilizaron un microscopio de fuerza atómica sobre una única hebra de ADN. Es una técnica notable que permite medir con precisión fuerzas entre moléculas del orden del pico-newton. Comparativamente las fuerzas ejercidas entre dos botellas de agua son de 20 newtones.
No obstante, las mediciones que realizaron no fueron sobre moléculas de ADN naturales, sino que sintetizaron dos tipos de moléculas, en un caso solamente con Adenina, y en el otro, únicamente con Timina. En el primer caso, se preveía que las atracciones entre nucleótidos serían más intensas mientras que para el de la Timina serían más débiles.
De hecho se observaron fuerzas de 23 y 113 pico-newtones y mientras que el BRIN de ADN formado de Timina tomaba una forma aleatoria, el de la Adenina tendía naturalmente a tomar forma de hélice, sugiriendo así que el origen de la forma de la molécula de la vida probablemente debía encontrarse en presencia de esta base. Sin embargo, todavía queda mucho que investigar.
 |
Un film para una gran audiencia. Nueve capítulos, dos horas de matemáticas, que nos llevan gradualmente hasta la cuarta dimensión. ¡Vértigo matemático garantizado!
Para cada capítulo hay la correspondiente información textual. En particular, hay versión en español para el capítulo 2, Cuarta dimensión, en el que M. C. Escher narra las aventuras de seres bidimensionales que tratan de imaginar objetos tridimensionales.
Audio en ingles; oportunidad de ver a los clasicos:
En esta oprtunidad tenemos las preguntas y sus respectivos solucionarios de la última Olimpiada Internacional de Física, realizada en Vietnam.
Primera Pregunta: theory_1_problem.
Solucionario: theory_1_solutionSegunda Pregunta: theory_2_problem.
Solucionario: theory_2_solution
Tercera Pregunta: theory_3_problem.
Solucionario: theory_3_solution
Prueba Experimental: experiment_problem.
Solucionario: experiment_solution1
Microscopio digital casero (EXPERIMENTO Para la helicociencia)
Publicado por gabriel1682010 en 16:18Sin embargo, tambien puedes construirte un sencillo microscopio digital con una webcam y una lente de la lunidad lectora de CD. Tan solo necesitas una cartulina de color negro (es muy importante) en la cual se debe hacer un pequeño orificio, menor al de la lente, sobre la cual pegaras a dicha lente. A su vez pegaras la cartulina a la webcam, para que la luz no entre al conjunto, haciendo coincidir las dos lentes. De esta forma la lente del CD-ROM actuará como una lupa, convirtiendo nuestra webcam en un microscopio.
Imagen de microscopio electronico de barrido (MEB) de una célula madre de médula ósea humana
Para realizar esta experiencia necesitarás:
- Programa generador de ondas (puedes bajarlo desde aquí); utilizen el server 2
- Altoparlante potenciado
- 1m2 de placa metálica o cartón corrugado
- Arroz o arena fina
Lo que debes hacer es lo siguiente:
- Instala el programa generador de ondas.
- Conecta el altoparlante a la salida de audio de la pc
- Coloca encima del parlante la placa metálica o cartón. Se logran mejores resultados con una bocina potente adherida directamente por debajo del centro de la placa.
- Comienza con una frecuencia baja y esparce el arroz sobre la placa.
- Ve aumentando gradualmente la frecuencia para observar los distintos patrones de interferencia de onda.
Las leyes básicas de la física funcionan igualmente bien hacia adelante que hacia atrás en el tiempo, pero percibimos el tiempo moviéndose sólo en una dirección, hacia el futuro. ¿Porqué?
Para dar cuenta de esto, debemos hurgar en la prehistoria del Universo, a un tiempo anterior al Big Bang. Nuestro Universo podría ser parte de un multiverso mucho mayor, que como un todo sea simétrico-temporal. El tiempo quizás vaya hacia atrás en otros universos.
El Universo no parece estar bien. Esto parece extraño de decir, dado que los cosmólogos tienen muy poco estándar para comparar. ¿Cómo sabemos cómo se supone que debería verse el Universo?
Sin embargo, a lo largo de los años, hemos desarrollado una fuerte intuición para lo que cuenta como “natural”, y el universo que vemos no califica.
No confundamos: los cosmólogos han armado una imagen increíblemente exitosa de cómo está formado el Universo y cómo evolucionó. Cerca de 14 mil millones de años atrás, el cosmos era más caliente y denso que el interior de una estrella y desde entonces se ha ido enfriando al expandirse. Esa imagen da cuenta de cada observación realizada, pero un número de características inusuales, especialmente en el Universo temprano, sugiere que hay más en la historia de lo que entendemos.
Entre los aspectos no naturales del Universo, uno sobresale: la asimetría temporal. Las leyes microscópicas de la física que yacen tras el comportamiento del Universo, no distinguen entre pasado y futuro, aunque el Universo temprano -caliente, denso, homogéneo- es completamente diferente del actual -frío, diluído, grumoso. El Universo comenzó ordenadamente y se ha vuelto progresivamente más desordenado desde entonces. La asimetría del tiempo, la flecha que apunta del pasado al futuro, juega un rol inconfundible en nuestras vidas cotidianas: da cuenta del porqué no podemos convertir un omelet en un huevo, porqué los cubitos de hielo nunca se forman espontáneamente en un vaso de agua y porqué recordamos el pasado pero no el futuro. Y el origen de la asimetría que experimentamos puede ser rastreada hasta el orden del Universo cerca del Big Bang. Cada vez que rompes un huevo, estás haciendo cosmología observacional.
La flecha del tiempo es posiblemente la característica más llamativa del universo que los cosmólogos están actualmente sin poder explicar.
Cada vez más, sin embargo, el rompecabezas acerca del Universo que observamos da pistas sobre la existencia de un espacio-tiempo mucho mayor que no vemos. Añade apoyo a la noción de que formamos parte de un multiverso cuya dinámica ayuda a explicar las aparentemente no-naturales características de nuestra vecindad local.
El rompecabezas de la Entropía
Los físicos encapsulan el concepto de asimetría del tiempo en la celebrada segunda ley de la termodinámica: la entropía en un sistema cerrado nunca decrece. Dicho grosso modo: la entropía es una medida del desorden de un sistema. En el Siglo XIX, el físico Ludwig Boltzmann explicó la entropía en términos de la distinción entre el microestado de un objeto y su macroestado. Si se le pide una descripción de una taza de café, Ud. probablemente se referiría a su macroestado -su temperatura, presión y otras características generales. El microestado, por otro lado, especifica la posición precisa y la velocidad de cada átomo individual en el líquido. Muchos diferentes microestados corresponden a algún macroestado particular: podemos mover un átomo aquí y allá, y nadie viendo a escalas macroscópicas lo notaría.
La entropía es el número de diferentes microestados que corresponden al mismo macroestado. (Técnicamente, es el número de dígitos, o logaritmo, de ese número). Así, hay más formas de ordenar un número dado de átomos en una configuración de alta entropía que en una de baja entropía. Imagine que derrama leche en su café. Hay muchas maneras de distribuir las moléculas para que la leche y el café estén completamente mezclados, pero relativamente pocas maneras de ordenarlas para separar la leche del café. Por lo que la mezcla tiene una entropía mayor.
Desde este punto de vista, no es sorprendente que la entropía tienda a crecer con el tiempo. Los estados de alta entropía superan grandemente a los de baja entropía; casi cualquier cambio en el sistema generará en un estado de entropía mayor. Ese es el porqué la leche se mezcla con el café pero nunca se des-mezcla. Aunque es físicamente posible para todas las moléculas de la leche conspirar espontáneamente para ordenarse a sí mismas una al lado de la otra, es estadísticamente muy improbable.
Si Ud. espera para que ocurra esto espontáneamente, debería esperar mucho más tiempo que la edad actual del universo observable. La flecha del tiempo es simplemente la tendencia de los sistemas a evolucionar hacia uno de los numerosos, naturales, estados de alta entropía.
Pero explicar porqué los estados de baja entropía evolucionan a estados de alta entropía es diferente de explicar porqué la entropía está incrementándose en nuestro universo. La pregunta permanece:¿Porqué la entropía fue baja al empezar? Parece poco natural, dado que los estados de baja entropía son tan raros. Incluso concediendo que el actual universo tiene una entropía media, eso no explica porqué la entropía solía ser incluso menor. De todas las posibles condiciones iniciales que podrían haber evolucionado hacia un Universo como el nuestro, la aplastante mayoría tiene mucha mayor entropía, no menor.[1]
En otras palabras, el verdadero reto no es explicar porqué la entropía del Universo será mayor mañana que hoy, sino explicar porqué la entropía fue menor ayer e incluso menor el día anterior. Podemos rastrear esta lógica hasta el comienzo del tiempo en nuestro universo observable. Finalmente, la asimetría del tiempo es una pregunta a responder por la cosmología.
El desorden del vacío
El Universo temprano era un lugar notable. Todas las partículas que forman el universo que observamos actualmente estaban apretadas en un volumen extraordinariamente caliente y denso. Más importante: estaban distribuidas casi uniformemente a través de ese pequeño volumen. En promedio, la densidad difería de un lugar a otro pero sólo en una parte en 100.000 aproximadamente. Gradualmente, al expandirse y enfriarse el universo, el tirón de la gravedad realzó esas diferencias. Regiones con más partículas formaron estrellas y galaxias, y regiones con menos partículas terminaron formando los vacíos.
Claramente, la gravedad ha sido crucial para la evolución del Universo. Desafortunadamente, no entendemos totalmente la entropía cuando la gravedad está involucrada. La gravedad surge de la forma del espacio-tiempo, pero no tenemos una teoría detallada del espacio-tiempo; ése es el objetivo de la teoría cuántica de la gravedad. Mientras que podemos relacionar la entropía de un fluído al comportamiento de las moléculas que lo constituyen, no sabemos qué constituye el espacio, por lo que no sabemos qué microestados gravitacionales corresponden a un macroestado particular.
Sin embargo, tenemos una idea de cómo la entropía evoluciona. En situaciones donde la gravedad es insignificante, como una taza de café, una distribución uniforme de partículas tiene una entropía alta. Esta condición es un estado de equilibrio. Incluso cuando las partículas se reordenan, están ya tan mezcladas que nada más parece ocurrir macroscópicamente. Pero si la gravedad es importante y el volumen es fijo, una suave distribución tiene relativamente baja entropía. En este caso, el sistema está muy lejos del equilibrio. La gravedad causa que las partículas se agrupen en estrellas y galaxias y la entropía crece notablemente, consistente con la segunda ley (de la termodinámica).
Efectivamente, si queremos maximizar la entropía de un volumen cuando la gravedad está activa, sabemos lo que obtendremos: un agujero negro. En los años 1970s Stephen Hawking de la Universidad de Cambridge confirmó una provocativa sugerencia de Jacob Bekenstein, ahora en la Universidad Hebrea de Jerusalem, de que los agujeros negros encajan nítidamente con la segunda ley. Al igual que los objetos calientes que la segunda ley describía originalmente, los agujeros negros emiten radiación y tienen entropía. Un montón de entropía. Un agujero negro de un millón de masas solares, como el que vive en el centro de nuestra galaxia, tiene 100 veces la entropía de todas las partículas ordinarias en el Universo observable.
Finalmente, incluso los agujeros negros se evaporan al emitir la radiación de Hawking. Un agujero negro no tiene la máxima entropía posible, sino la mayor entropía que puede ser empaquetada en cierto volumen. El volumen del espacio en el Universo, sin embargo, parece estar creciendo sin límite. En 1998 los astrónomos descubrieron que la expansión cósmica se está acelerando. La explicación más simple es la existencia de la energía oscura, una forma de energía que existe incluso en el espacio vacío y que no se diluye al expandirse el Universo. No es la única explicación para la aceleración cósmica, pero los intentos de llegar a una idea mejor han fallado hasta ahora.
Si la energía oscura no se diluye, el universo se expanderá para siempre. Las galaxias distantes desaparecerán de la vista. [2]
Aquellas que no colapsen en agujeros negros, se evaporarán en la oscuridad circundante como un charco se seca en un día caluroso. Lo que quedará es un universo que, para todo intento y propósito, será vacío. Entonces, y sólo entonces, el universo habrá verdaderamente maximizado su entropía. El universo estará en equilibrio, y nada más ocurrirá.
Puede parecer raro que el espacio vacío tenga una entropía tan enorme. Suena como decir que el escritorio más desorganizado en el mundo es un escritorio completamente vacío. La entropía requiere microestados y, a primera vista, el espacio vacío no tiene ninguno. Sin embargo, el espacio vacío tiene un montón de microestados - los microestados cuántico-gravitacionales de la fábrica del espacio. No sabemos aún qué son exactamente estos estados, nada más sabemos que los microestados dan cuenta de la entropía de un agujero negro, pero sí sabemos que en un universo en aceleración la entropía en el volumen observable se acerca a un valor constante proporcional al área de su frontera. Es una cantidad verdaderamente enorme de entropía, mucho más que la materia en ese volumen.
Pasado vs. Futuro
La característica más increíble de esta historia es la pronunciada diferencia entre el pasado y el futuro. El universo comienza en un estado de muy baja entropía: partículas empaquetadas juntas de forma suave. Evoluciona a un estado de entropía medio: la grumosa distribución de estrellas y galaxias que vemos a nuestro alrededor actualmente. Finalmente alcanza un estado de alta entropía: el espacio casi vacío, presentando sólo alguna ocasional partícula de baja energía.
¿Porqué son el pasado y el futuro tan diferentes? No es suficiente proponer simplemente una teoría de condiciones iniciales - una razón de porqué el universo comenzó con baja entropía. Como el filósofo Huw Price de la Universidad de Sydney apuntó, cualquier razonamiento que aplique a las condiciones iniciales debería también aplicar a las condiciones finales, o de lo contrario seremos culpables de asumir la misma cosa que estábamos tratando de probar - que el pasado fue especial. O bien debemos tomar la profunda asimetría del tiempo como una abrupta característica del universo que escapa a la explicación, o debemos indagar más profundamente en el funcionamiento del espacio y el tiempo.
Muchos cosmólogos han intentado atribuir la asimetría del tiempo al proceso de la inflación cosmológica. La inflación es una atractiva explicación para muchas características básicas del universo. De acuerdo a esta idea, el universo muy temprano (o al menos una parte de éste) estaba lleno no de partículas sino con una forma temporaria de energía oscura, cuya densidad era enormemente mayor que la energía oscura que observamos hoy. Esta energía causó la expansión del universo a una tasa de aceleración fantástica, luego de lo cual decayó hacia materia y radiación, dejando detrás un pequeño resto de energía oscura que se está haciendo relevante otra vez en la actualidad. El resto de la historia del Big Bang, del suave gas primordial a las galaxias y más allá, se sigue simplemente.
La motivación original para la inflación fue proveer una robusta explicación para las afinadas condiciones en el universo temprano -en particular, la notable uniformidad de la densidad de la materia en regiones ampliamente separadas. La aceleración generada por la energía oscura temporal suavizó al universo casi perfectamente. La anterior distribución de materia y energía es irrelevante; una vez que la inflación comenzó, removió cualquier trazo de condiciones preexistentes, dejándonos con un caliente, denso y suave universo temprano.
El paradigma inflacionario ha sido exitoso en muchas formas. Su predicción de pequeñas desviaciones de la uniformidad perfecta está de acuerdo con las observaciones de variaciones de densidad en el universo. Como una explicación para la asimetría del tiempo, sin embargo, los cosmólogos la consideran cada vez más un poco engañosa, por razones que Roger Penrose de la Universidad de Oxford y otros han enfatizado. Para que el proceso trabaje como se desea, la ultradensa energía oscura debió comenzar en una configuración específica. De hecho, su entropía debió ser fantásticamente menor que la entropía del gas caliente y denso en el que decayó. Esto implica que la inflación no resolvió verdaderamente nada: “explica” un estado de inusual baja entropía (un caliente, denso, uniforme gas) al invocar un estado anterior de aún menor entropía (una suave porción de espacio dominado por energía oscura ultradensa). Simplemente empuja el rompecabezas un paso atrás:¿Porqué la inflación ocurrió alguna vez?
Una de las razones por la que muchos cosmólogos invocan la inflación como una explicación de la asimetría del tiempo es que la configuración inicial de la energía oscura no parece tan improbable. Todo el tiempo de la inflación, nuestro universo observable fue menos de un centímetro de lado. Intuitivamente, semejante pequeña región no tiene muchos microestados, por lo que no es tan improbable para el universo tropezar por accidente en un microestado correspondiente a la inflación.
Desafortunadamente, esta intuición es engañosa. El universo temprano, incluso si es de sólo un centímetro de lado, tiene exactamente el mismo número de microestados que todo el universo observable actual. De acuerdo a las reglas de la mecánica cuántica, el número total de microestados en un sistema nunca cambia (La entropía crece no porque el número de microestados lo hace sino porque el sistema naturalemente termina en el más genérico macroestado posible). De hecho, el universo temprano es el mismo sistema físico que el universo tardío. Uno evoluciona hacia el otro, después de todo.
Entre todas las diferentes maneras que los microestados del universo pueden ordenarse, sólo una increíblemente pequeña fracción corresponde a una configuración suave de ultradensa energía oscura en un pequeño volumen. Las condiciones necesarias para que la inflación comience son extremadamente especializadas y así describe una configuración de muy baja entropía. Si Ud. debe elegir configuraciones del universo al azar, sería muy improbable dar con las condiciones para iniciar la inflación. La inflación no explica, por sí misma, porqué el universo temprano tiene una baja entropía, simplemente lo asume desde el comienzo.
Un Universo Simétrico en el Tiempo
Así, la inflación no ayuda a explicar porqué el pasado es diferente del futuro. Una valiente pero simple estrategia es decir: quizás el pasado muy lejano no sea diferente del futuro, después de todo. Quizás el pasado distante, como el futuro, es en realidad un estado de alta entropía. Si es así, el caliente, denso estado que hemos estado llamando “el universo temprano” no es en realidad el verdadero comienzo del universo sino un estado transicional entre estados de su historia.
Algunos cosmólogos imaginan que el universo pasó por un “rebote”. Antes de este evento, el espacio estaba en contracción, pero en vez de chocar en un punto de infinita densidad, nuevos principios físicos -gravedad cuántica, dimensiones extras, teoría de cuerdas o algún otro exótico fenómeno- lo salvó en el último minuto y el universo salió hacia el otro lado en lo que ahora percibimos como el big bang. Aunque intrigante, las cosmologías “del rebote” no explican la flecha del tiempo. O bien la entropía estaba incrementándose al acercarse el universo previo al choque (crunch) -en cuyo caso la flecha del tiempo se extiende infinitamente lejos en el pasado- o la entropía estaba decreciendo, en cuyo caso una no natural condición de baja entropía ocurrió en la mitad de la historia del universo (en el rebote). De cualquier manera, hemos dejado de contestar porqué la entropía cerca de lo que llamamos big bang fue pequeña. (NdA:Ver ¿Qué pasó antes del Big Bang?)
En cambio, supongamos que el universo comenzó en un estado de gran entropía, que es el estado más natural. Un buen candidado para semejante estado es un espacio vacío. Como cualquier estado de alta entropía, la tendencia del espacio vacío permanecerá así, sin cambios. Por lo que el problema es:¿Cómo obtenemos nuestro universo actual de un desolado y tranquilo espacio-tiempo? El secreto podría residir en la existencia de la energía oscura.
En presencia de energía oscura, el espacio vacío no es completamente vacío. Fluctuaciones de campos cuánticos dan lugar a una temperatura muy baja - enormemente más baja que la temperatura del universo actual pero no exactamente el cero absoluto. Todos los campos cuánticos experimentan fluctuaciones térmicas en ese universo. Eso significa que no es perfectamente inactivo; si esperamos lo suficiente, partículas individuales e inclusive sustanciales colecciones de partículas fluctuarán hacia su existencia, sólo para desaparecer otra vez en el vacío. (Estas son partículas reales, en oposición a las partículas “virtuales” de corta vida que el espacio vacío contiene incluso en ausencia de energía oscura).
Entre las cosas que pueden fluctuar hacia la existencia están las pequeñas regiones de energía oscura ultradensa. Si las condiciones son las correctas, esa región puede sufrir la inflación y cerrarse para formar un universo separado por su cuenta - un universo bebé. Nuestro universo podría ser el hijo de otro universo.
Superficialmente, este escenario tiene un parecido con la inflación estándar. La diferencia es la naturaleza de las condiciones iniciales. En la forma estándar, la región surge en un enfervorizante universo fluctuante, en el que la mayor parte de las fluctuaciones produjeron nada parecido a la inflación. Sería mucho más probable para el universo, fluctuar directamente en un big bang caliente, salteándose el estadío inflacionario completamente. De hecho, en cuanto concierne a la entropía, sería mucho más probable para el universo fluctuar directamente hacia la configuración que vemos hoy, sorteando los pasados 14 mil millones de años de evolución cósmica.
En nuestro nuevo escenario, el universo preexistente no fue nunca fluctuante al azar; estaba en un estado muy específico: espacio vacío. Lo que esta teoría afirma - y que debe probarse- es que la manera más probable de crear universos como el nuestro de un estado preexistente es ir a través de un período de inflación, en vez de fluctuar directamente. Nuestro univeso, en otras palabras, es una fluctuante pero no uno azaroso.
Opmeit Led Ahcelf
Este escenario, propuesto en 2004 por Jennifer Chen de la Universidad de Chicago y yo, provee una provocativa solución al origen de la asimetría en nuestro universo observable: vemos sólo una pequeña parte de toda la imagen, y ese campo mayor es simétrico en el tiempo. La entropía puede crecer sin límite a través de la creación de nuevos univesos.
Aún mejor, esta historia puede ser contada hacia atrás y hacia adelante en el tiempo. Imagine que empezamos con espacio vacío en cierto momento particular y lo vemos evolucionar hacia el futuro y hacia el pasado. (Va hacia ambos lados porque no estamos presumiendo una unidireccional flecha del tiempo). Los bebés universos fluctúan hacia la existencia en ambas direcciones del tiempo, finalmente vaciándose y dando a luz sus propios bebés. A escalas ultragrandes, semejante multiverso se vería estadísticamente simétrico con respecto al tiempo - ambos, pasado y futuro, tendrían nuevos universos fluctuando hacia la vida y proliferando. Cada uno de ellos experimentaría una flecha del tiempo, pero la mitad tendrían una flecha que estaría en reversa con respecto a la flecha de otros.
La idea de un universo con una flecha del tiempo hacia atrás podría parecer alarmante. Si conociéramos a alguien de un univeso así, ¿se acordarían del futuro? Felizmente, no hay peligro para tal encuentro. En el escenario que estamos describiendo, los únicos lugares donde el tiempo parece ir hacia atrás están enormemente lejos en nuestro pasado, mucho antes del big bang. En medio hay una amplia expansión del universo en la que el tiempo no parece correr en absoluto; casi no existe materia y la entropía no evoluciona. Cualquier ser que viva en una de estas regiones de tiempo revertido no nacería viejo y moriría joven, ni nada fuero de lo ordinario. Para ellos, el tiempo fluiría en una forma convencional. Sería sólo al comparar su universo con el nuestro que algo parecería fuera de lo normal: nuestro pasado es su futuro y viceversa. Pero semejante comparación es puramente hipotética, ya que no podemos llegar allí y ellos no pueden llegar aquí.
Por ahora, el jurado está fuera de nuestro modelo. Los cosmólogos han contemplado la idea de bebés universos por muchos años, pero no entendemos el proceso de nacimiento. Si las fluctuaciones cuánticas pudieran crear nuevos universos, también podrían crear muchas otras cosas - por ejemplo, una galaxia entera. Para que un escenario como el nuestro explique el universo que vemos, debe predecir que la mayoría de las galaxias surgen en el período posterior al big bang - como eventos y no sólo fluctuaciones en otro universo vacío. Si no, nuestro universo parecería muy anormal.
Pero la lección para llevarnos a casa no es un escenario particular para la estructura del espacio-tiempo a ultragrandes escalas. Es la idea que una increíble característica de nuestro cosmos observable - la flecha del tiempo, surgiendo de condiciones de muy baja entropía en el universo temprano- puede proveernos pistas acerca de la naturaleza del universo no-observable.
Como se mencionó al principio de este artículo, es bueno tener una imagen que concuerde con los datos, pero los cosmólogos quieren más que eso: buscamos un entendimiento a las leyes de la naturaleza y de nuestro particular univeso en la que todo tenga sentido para nosotros. No queremos ser reducidos a aceptar las extrañas características de nuestro universo como hechos brutos. La dramática asimetría del tiempo de nuestro cosmos observable parece ofrecernos una pista sobre algo más profundo -un clave hacia el funcionamiento esencial del espacio y el tiemp. Nuestra tarea como físicos es usar esta y otras pistas para armar una poderosa imagen.
Si el universo observable fuera todo lo que existe, sería casi imposible dar cuenta de la flecha del tiempo en una forma natural. pero si el universo a nuestro alrededor es un pequeña parte de una imagen mucho mayor, nuevas posibilidades se presentan. Podemos concebir nuestro porción de universo como una pieza de un rompecabezas, parte de la tendencia de un sistema mayor para incrementar su entropía sin límites en el pasado lejano y el futuro distante. Parafraseando al físico Edward Tyron, el big bang es fácil de entender si no es el comienzo de todo sino una de esas cosas que ocurren de tiempo en tiempo.
Otros investigadores están trabajando en ideas similares, y más y más cosmólogos están tomando seriamente el problema que genera la flecha del tiempo. Es suficientemente fácil ver la flecha -todo lo que debe hacer es mezclar un poco de leche a su café. Mientras lo revuelve, puede contemplar cómo es simple acto puede ser rastreado todo el camino hacia el comienzo de nuestro universo observable y quizás más allá.
Aquí hay una línea de tiempo de los eventos importantes en la historia de nuestro universo observable, de acuerdo a la cosmología convencional:
-El espacio está vacío, caracterizándose sólo por una pequeña cantidad de energía de vacío y una ocasional partícula de larga longitud de onda formada vía fluctuaciones de los campos cuánticos que tiñen el espacio.
-Una radiación de alta intensidad barre de pronto el universo, en una forma esférica enfocándose en un punto en el espacio. Cuando la radiación colecta todo en ese punto, un “agujero blanco” se formó.
-El agujero blanco gradualmente crece a miles de millones de veces la masa del sol, a través de la acreción de radiación adicional de la decreciente temperatura.
-Otros agujeros blancos comienzan a aproximarse desde miles de millones de años luz. Forman una distribución homogénea, moviéndose lentamente uno hacia el otro.
-Los agujeros blancos comienzan a perder masa al eyectar gas, polvo y radiación al entorno circundante.
-El gas y polvo ocasionalmente implosionan para formar estrellas, que se esparcen hasta galaxias alrededor de los agujeros blancos.
-Como los agujeros blancos, las estrellas reciben radiación. Usan la energía de esta radiación para convertir elementos pesados en otros más livianos.
Las estrellas se dispersan en gas, que gradualmente se suaviza a través del espacio; la materia como un todo continúa moviéndose junta y crece más densamente.
-El universo se vuelve cada vez más caliente y denso, finalmente contrayéndose hacia un big crunch.
Es innecesario decir que esta no es la forma usual de describir la historia de nuestro universo. Es la secuencia convencional de eventos contados hacia atrás en el tiempo. Pero las leyes de la física trabajan igualmente bien hacia atrás y hacia adelante en el tiempo. Así, esta secuencia es tan legítima como la usual. Sirve al propósito de llevar a casa cuán improbable es realmente la historia de nuestro universo observable.
S.M.C.
Preguntas frecuentes de La Flecha del Tiempo
Si la entropía siempre se incrementa, ¿cómo se forman los objetos de baja entropía?
La ley de entropía se aplica a sistemas cerrados. No prohibe el decrecimiento de la entropía en sistemas abiertos, incluyendo gallinas. Una gallina toma energía y realiza un gran esfuerzo en producir un huevo.
¿Ningún proceso de partículas tiene una flecha del tiempo?
El decaimiento de algunas partículas elementales, como los kaons neutrales, ocurren más frecuentemente en una dirección del tiempo que en otra. (Los físicos no necesitan viajar atrás en el tiempo para observar esta asimetría, ellos infieren esto de experimentos sobre propiedades de las partículas). Pero estos procesos son reversibles, a diferencia del crecimiento de la entropía, por lo que no explican la flecha del tiempo. El modelo estándar de la física de partículas no parece ser de ayuda en explicar la baja entropía del universo temprano.
¿La mecánica cuántica tiene una flecha del tiempo?
De acuerdo a la interpretación estándar de la mecánica cuántica, la medición de un sistema causa una función de onda que “colapsa”, un proceso que es asimétrico en el tiempo. Pero la razón de que las funciones de onda colapsen pero nunca “des-colapsen” es la misma razón por la que los huevos se rompen y no se “des-rompen”, porque el colapso incrementa la entropía del universo. La mecánica cuántica no explica porqué la entropía fue baja en primer lugar.
¿Porqué recordamos el pasado y no el futuro?
Formar una memoria confiable requiere que el pasado esté ordenado - esto es, tenga una baja entropía. Si la entropía es alta, casi todos los “recuerdos” serían fluctuaciones al azar, completamente desvinculadas de lo que realmente pasó en el pasado.
¿Es testeable la teoría del multiverso?
La idea de que el univeso se extiende mucho más allá de lo que vemos no es realmente una teoría - es una predicción hecha por ciertas teorías de la mecánica cuántica y gravedad. La verdad es que es una predición difícil de probar. Pero todas las teorías de la física nos fuerzan a ir más allá de lo que podemos ver directamente. Por ejemplo, nuestro mejor modelo actual para el origen de la estructura cósmica, el escenario inflacionario, requiere que entendamos las condiciones incluso antes de la inflación.
El cosmólogo Max Tengmark dice que las fórmulas matemáticas crean la realidad.
Los cosmólogos no son pensadores comunes y Max Tengmark no lo es. En una serie de documentos que captaron la atención de físicos y filósofos alrededor del mundo, explora no lo que dicen las leyes de la naturaleza sino sobre el porqué existen estas leyes.
De acuerdo a Tegmark, “todo lo que existe es matemáticas”. En su teoría, la hipótesis del universo matemático, actualiza la física cuántica y la cosmología con el concepto de muchos universos paralelos habitando en múltiples niveles del espacio y tiempo. Al posar su hipótesis en el cruce entre la física y la filosofía, se remonta a la clásica pregunta de los Griegos:¿Qué es real?
El científico prosiguió con su hipótesis, a sabiendas de que tan alocada idea podría perjudicar su reputación. Pero empujado por su optimismo y pasión, continuó adelante.
“Aprendí rápidamente que si me enfocaba exclusivamente en estas grandes cuestiones terminaría trabajando en McDonalds”, dice Tegmark y continúa: “Así que desarrollé una estrategia de Dr. Jekyll y Mr. Hyde en la que, al aplicar para un trabajo, ponía de relieve mi trabajo principal. Y luego, por mi lado, perseguía intereses más filosóficos”. Hoy es profesor en el Instituto de Tecnología de Massachusetts y tiene una buena reputación entre los mejores físicos del mundo.
En estos días, Tegmark es un hombre ocupado. Con su esposa, la cosmóloga brasilera Angelica de Oliveira-Costa, equilibra la ciencia con la demanda de criar dos jóvenes chicos. El entrevistador es el astrofísico teórico Adam Frank de la Universidad de Rochester, Nueva York.
Max, tú has ganado una reputación por pensar en cuestiones fuera de lo común, incluso para un cosmólogo. ¿Siempre has reflexionado sobre cuestiones profundas como la vida, el Universo y Todo lo demás?
No. Estaba muy confudido de joven. Llegué a eso bastante tarde y no había nadie con quien hablar de filosofía cuando era adolescente. Tenía un amigo en la secundaria que hacía las cosas de forma opuesta a los demás. Si la gente mandaba cartas en sobres rectangulares, él habría hecho sobres triangulares. Recuerdo el pensar:”Eso está bueno. Así es como quiero ser”.
¿Es por eso que decidiste ir hacia la física?
En realidad, mi padre es un matemático y siempre era de alentarme acerca de las matemáticas, pero la física era aburrida en la secundaria. Así comencé a estudiar economía.
Esa fue una elección interesante. ¿Cuándo reapareció la física otra vez?
Un amigo me dio un libro, Seguramente está bromeando, Mr. Feynman (“Surely You’re Joking, Mr. Feynman!”) por el físico Richard Feynman. Era sobre elegir casilleros y chicas. No tenía nada que ver con la física, pero entre líneas decía fuerte y claro “Amo la física!”. No podía entender cómo eso era la misma materia aburrida de la secundaria. Realmente me picó la curiosidad.
¿De qué forma?
Si tú ves un hombre mediocre caminando en la calle del brazo de Cameron Díaz, te dices a tí mismo:”Me estoy perdiendo algo aquí”. Así que empecé a leer las conferencias de Feynman sobre física y estaba como..whoa! ¿cómo no me dí cuenta antes de esto?
¿Así que cambiaste de carrera?
Umm, no. No se paga el colegio en Suecia, por lo que fui capaz de enrolarme en una universidad diferente para hacer física sin decirles que ya estaba estudiando economía.
¿Fuiste a dos universidades al mismo tiempo?
Yeah. Como puedes ver, estaba confundido. Se me complicó en algunos momentos. Tenía exámenes en ambos lugares el mismo día, y tenía que ir en bicicleta realmente rápido.
¿Fue en la universidad donde comenzaste a pensar acerca de las grandes cuestiones?
Estaba tomando la única clase de física cuántica ofrecida y cuando llegué al capítulo sobre las mediciones sentí que seguramente me estaba perdiendo algo.
Te refieres acerca de cómo el observador parece afectar la medición de lo que está siendo observado.
Correcto. Existe esta bella ecuación matemática en la teoría cuántica llamada ecuación de Schrödinger. Usa algo llamado la función de onda para describir el sistema que estás estudiando -un átomo, un electrón, lo que sea- y todas las formas posibles en que el sistema puede evolucionar. La perspectiva usual de la mecánica cuántica es que en cuanto mides algo, la función de onda literalmente colapsa, pasando de un estado que refleja todos los resultados posibles a un estado que refleja sólo uno: el resultado que ves en el momento en que la medición se realizó. Parecía loco para mí. No entendía porqué se suponía que usara la ecuación de Schrödinger antes de medir el átomo, pero luego, al medirlo, la ecuación no aplicaba. Por lo que tomé coraje y golpeé la puerta de uno de los físicos más famosos en Suecia, un hombre en el comité Nobel, pero me hechó. No fue hasta años después que tuve esta revelación de que no era yo quien no lo entendía, era él!
Es un bello momento en la educación de un científico cuando te das cuenta que estas personas en posiciones más altas de poder no tienen todas las respuestas. Por lo que tomaste tus preguntas acerca de la ecuación de Schrödinger y el efecto en las mediciones contigo cuando partiste a los Estados Unidos y tu doctorado en Berkeley
Allí fue donde comenzó todo para mí. Tenía este amigo, Bill Poirier, y pasamos horas hablando sobre ideas locas en física. Me ponía nervioso porque yo argumentaba que cualquier descripción fundamental del universo debería ser simple. Para molestarlo, decía que podría haber un universo entero que fuera nada más que un dodecaedro, una figura de doce lados que los Griegos describieron 2500 años atrás. Por supuesto, sólo lo estaba embromando, pero luego, cuando pensé más en ello, me emocioné acerca de la idea de que el universo fuera realmente nada más que un objeto matemático. Eso me dejó pensando que cada objeto matemático es, en un sentido, su propio universo.
Desde el comienzo intentaste publicar esta idea radical. ¿Te preocupaste acerca de si afectaría a tu carrera?
Anticipé problemas y no envié hasta haber aceptado una cita posdoctoral en la Universidad Princeton. Mi primer paper fue rechazado por tres revistas. Finalmente conseguí una un reporte de buena referencia de Annals of Physics, pero el editor lo rechazó por ser muy especulativo.
Espera…eso no se supone que ocurra. Si un referí gusta de un paper, usualmente es aceptado.
Eso es lo que pensé. Fui afortunado en ser amigo de John Wheeler, un físico teórico en Princeton y uno de mis mayores héroes en física, quien recientemente falleció. Cuando le mostré la carta de rechazo, él dijo:”Extremadamente especulativo? Bah!” Luego me recordó que algunos de los papers originales de mecánica cuántica también fueron considerados extremadamente especulativos. Por lo que escribí una apelación a Annals of Physics e incluí los comentarios de Wheeler. Finalmente, los editores lo publicaron.
Aún así, no era tu medio de vida. Hiciste tu doctorado y postdoc en cosmología, un tema totalmente distinto.
Es irónico que mi protección para estos intereses más filosóficos fue la cosmología, un campo que usualmente fue visto como excéntrico también. Pero la cosmología se fue gradualmente más respetable porque la tecnología informática, del espacio y de detección se combinaron para darnos una avalancha de fabulosa información acerca del universo.
Hablemos de tu esfuerzo por entender el problema de la medición al proponer universos paralelos -o como los llamas en total, el multiverso. ¿Puedes explicar universos paralelos?
Hay cuatro niveles distintos de multiverso. Tres de ellos han sido propuestos por otras personas, y yo añadí el cuarto, el universo matemático.
Si necesitas estos textos no duden en comunicarse conmigo, esta es la relación:
MECÁNICA CLÁSICA
- Classical Mechanics - R. Douglas Gregory
- Classical Mechanics - Tom W B Kibble, Frank H Berkshire
- Classical Mechanics Systems of Particles and Hamiltonian Dynamics - Walter Greiner
- Classical Mechanics: Point Particles and Relativity (Classical Theoretical Physics) - Walter Greiner
- Introduction to Classical Mechanics: With Problems and Solutions - David Mori
- A History Electricity and Magnetism - Herbert W. Meyer
- Advances in Electromagnetic Fields in Living Systems: Volume 4 (Advances in Electromagnetic Fields in Living Systems) - James C. Lin
- Antenna Theory & Design (IEEE Press Series on Electromagnetic Wave Theory) - Robert S. Elliott
- Applied Electromagnetics and Electromagnetic Compatibility (Wiley Series in Microwave and Optical Engineering) - Dipak L. Sengupta, Valdis V. Liepa
- Atoms In Electromagnetic Fields (World Scientific Series on Atomic, Molecular and Optical Physics) - Claude Cohen-Tannoudji
- Basic Electromagnetism and Materials (AIP Conference Proceedings)
- Beginning Physics II: Waves, Electromagnetism, Optics and Modern Physics
- Classical Electromagnetic Theory (Fundamental Theories of Physics) - Jack VanderLinde
- Collective Electrodynamics: Quantum Foundations of Electromagnetism - Carver A. Mead
- Conformal Array Antenna Theory and Design (IEEE Press Series on Electromagnetic Wave Theory)
- Differential Forms in Electromagnetics (IEEE Press Series on Electromagnetic Wave Theory) - Ismo V. Lindell
- Electricity and Magnetism - Munir H. Nayfeh, Morton K. Brussel
- Electromagnetic Absorption in the Copper Oxide Superconductors (Selected Topics in Superconductivity)
- Electromagnetic Compatibility of Integrated Circuits: Techniques for low emission and susceptibility
- Electromagnetic Field and Relativistic Particles (International Series in Pure and Applied Physics)
- Electromagnetic Field Theory Fundamentals - Bhag Singh Guru, Hüseyin R. Hiziroglu
- Electromagnetic Fields (IEEE Press Series on Electromagnetic Wave Theory)
- Electromagnetic Fields and Waves: Including Electric Circuits
- Electromagnetic Metamaterials: Transmission Line Theory and Microwave Applications
- Electromagnetic Modeling by Finite Element Methods (Electrical Engineering and Electronic Series, 117)
- Electromagnetic Propagation in Multi-Mode Random Media - Harrison E. Rowe
- Electromagnetic Radiation: Variational Methods, Waveguides and Accelerators
- Electromagnetic Scattering using the Iterative Multi-Region Technique
- Electromagnetic Theory and Applications for Photonic Crystals
- Electromagnetic Theory for Microwaves and Optoelectronics - Keqian Zhang, Dejie Li
- Electromagnetics (Electrical Engineering Textbook Series)
- Electromagnetics in Biology - Masamichi Kato
- Electroweak Theory - E. A. Paschos
- Establishing a Dialogue on Risks from Electromagnetic Fields
- Foundations of Electromagnetic Theory - John R. Reitz, Frederick J. Milford
- Fundamentals of Magnetism - Mathias Getzlaff
- Gauge Theories of the Strong, Weak and Electromagnetic Interactions (Advanced Book Classics)
- Genetic Algorithms in Electromagnetics - Randy L. Haupt
- Handbook of Engineering Electromagnetics - Rajeev Bansal
- Introduction to Electromagnetic Compatibility (Wiley Series in Microwave and Optical Engineering) - Clayton R. Paul
- Introductory Electromagnetics
- Introductory Electromagnetics - Zoya Popovic, Branko D. Popovic
- Magnetic Resonance Imaging: Physical Principles and Applications (Electromagnetism) - Vadim Kuperman
- Magnetism and Structure in Functional Materials (Springer Series in Materials Science) - A. Planes, L. Mañosa, A. Saxena
- Magnetism in Condensed Matter (Oxford Maser Series in Condensed Matter Physics) - Stephen Blundell
- Magnetism: A Synchrotron Radiation Approach (Lecture Notes in Physics) - Eric Beaurepaire, Hervé Bulou, Fabrice Scheurer, Jean-Paul Kappler
- Magnetism: Fundamentals - Etienne du Trémolet de Lacheisserie, Damien Gignoux, Michel Schlenker
- Magnetism: Materials and Applications - Etienne du Trémolet de Lacheisserie, Damien Gignoux, Michel Schlenker
- Problems and Solutions on Electromagnetism (Major American Universities Ph.D. Qualifying Questions and Solutions)
- Radiation and Scattering of Waves (IEEE Press Series on Electromagnetic Wave Theory)
- Scattering of Electromagnetic Waves: Theories and Applications
- Schaum’s Outline of Electromagnetics - Joseph Edminister
- Spheroidal Wave Functions in Electromagnetic Theory (Wiley Series in Microwave and Optical Engineering) - Le-Wei Li, Xiao-Kang Kang, Mook-Seng Leong
- The Electromagnetic Origin Of Quantum Theory And Light - Dale M. Grimes, Craig A. Grimes
- The Finite Difference Time Domain Method for Electromagnetics
- A Course in Modern Mathematical Physics: Groups, Hilbert Space and Differential Geometry
- A Unified Grand Tour of Theoretical Physics, 2nd edition
- Advanced General Relativity (Cambridge Monographs on Mathematical Physics) - John Stewart
- Advanced Mathematical Methods for Scientists and Engineers (International Series in Pure and Applied Mathematics) - Carl M. Bender, Steven A. Orszag
- Analytic Methods in Physics - Charlie Harper
- Applied Analysis - Cornelius Lanczos
- Applied Mathematical Methods in Theoretical Physics - Michio Masujima
- Basic Theoretical Physics: A Concise Overview - Uwe Krey, Anthony Owen
- Clifford Algebra: A Computational Tool for Physicists - John Snygg
- Computer Algebra Recipes for Mathematical Physics
- Cosmic Strings and Other Topological Defects (Cambridge Monographs on Mathematical Physics) - A. Vilenkin, E. P. S. Shellard
- Differential Geometry and Lie Groups for Physicists
- Differential Geometry and Topology of Curves
- Differential Geometry in Physics (Lecture Notes)
- Differential Geometry, Lie Groups, and Symmetric Spaces (Pure and Applied Mathematics,Vol 80)
- Equations of Mathematical Physics
- Essential Mathematical Methods for Physicists - Hans J. Weber, George B. Arfken
- Explorations in Mathematical Physics: The Concepts Behind an Elegant Language - Don Koks
- Finite Element Methods for Maxwell’s Equations (Numerical Analysis and Scientific Computation Series) - Peter Monk
- Finite Elements and Fast Iterative Solvers: with Applications in Incompressible Fluid Dynamics (Numerical Mathematics and Scientific Computation)
- Fourier Series, Transforms and Boundary Value Problems
- Free Boundary Problems (International Series of Numerical Mathematics)
- Free Energy and Self-Interacting Particles (Progress in Nonlinear Differential Equations and Their Applications) - Takashi Suzuki
- General Relativity for Mathematicians (Graduate Texts in Mathematics) - R.K. Sachs, H.-H. Wu
- Geometrical Methods in Mathematical Physics - Bernard F. Schutz
- Gravitation and Cosmology: From the Hubble Radius to the Planck Scale
- Interacting Electrons and Quantum Magnetism
- Introduction to String Field Theory
- Lectures on Non-Perturbative Canonical Gravity
- Lie Algebras in Particle Physics (Frontiers in Physics) - Howard Georgi
- Lie groups for physicists (The Mathematical physics monograph series)
- Linear Differential Operators - Cornelius Lanczos
- Lorentzian Wormholes: From Einstein to Hawking (AIP Series in Computational and Applied Mathematical Physics)
- Mathematical and Physical Data, Equations, and Rules of Thumb
- Mathematical Methods for Physicists - George B. Arfken
- Mathematical Methods for Physics and Engineering: A Comprehensive Guide
- Mathematical Methods in the Physical Sciences, Second Edition - Mary L. Boas
- Mathematical Perspectives on Theoretical Physics: A Journey from Black Holes to Superstrings
- Mathematical Physics - S. Rahvar, N. Sadooghi
- Mathematical Physics by Eugene Butkov
- Mathematical Physics: A Modern Introduction to Its Foundations - Sadri Hassani
- Matrices: Theory and Applications - Denis Serre
- Mechanics of Material Forces (Advances in Mechanics and Mathematics) - Paul Steinmann, Gérard A. Maugin
- Methods for Solving Mathematical Physics Problems
- Methods of Celestial Mechanics: Volume I: Physical, Mathematical, and Numerical Principles (Astronomy and Astrophysics Library) - Gerhard Beutler
- Methods of Mathematical Physics, Vol. 1 - R. Courant, D. Hilbert
- Methods of Mathematical Physics, Vol. 2 - R. Courant, D. Hilbert
- Modern Density Functional Theory: A Tool For Chemistry - J.M. Seminario, P. Politzer
- Modern Differential Geometry for Physicists (World Scientific Lecture Notes in Physics)
- Numerical Methods for Engineers and Scientists, Second Edition
- Operator Algebras and Quantum Statistical Mechanics 1: C*- and W*-Algebras. Symmetry Groups. Decomposition of States (Theoretical and Mathematical Physics)
- Optimization Algorithms in Physics - Alexander K. Hartmann, Heiko Rieger
- Path Integral Quantization and Stochastic Quantization (Springer Tracts in Modern Physics) - Michio Masujima
- Path Integrals and Their Applications in Quantum Statistical and Solid State Physics
- Physical Problems Solved by the Phase-Integral Method - Nanny Fröman, Per Olof Fröman
- Planar Ising Correlations (Progress in Mathematical Physics) - John Palmer
- Problems and Solutions in Theoretical and Mathematical Physics: Advanced Level - Willi-Hans Steeb
- Quantum Field Theory in Condensed Matter Physics (Theoretical and Mathematical Physics) - Naoto Nagaosa, S. Heusler
- Quantum Information Theory and Quantum Statistics (Theoretical and Mathematical Physics) - Dénes Petz
- Quantum Magnetism (Lecture Notes in Physics)
- Quarks, Leptons and the Big Bang
- Quaternions, Clifford Algebras and Relativistic Physics - Patrick R. Girard
- Selected Problems in Theoretical Physics
- Statistical Mechanics: From First Principles to Macroscopic Phenomena
- Statistical Physics - Akira Isihara
- Supersymmetric Quantum Cosmology (Cambridge Monographs on Mathematical Physics) - P. D. D’Eath
- Tensor Analysis - L.P. Lebedev, Michael J. Cloud
- Tensors and Manifolds: with Applications to Mechanics and Relativity - Robert H. Wasserman
- The Geometry of Physics: An Introduction - Theodore Frankel
- The Mathematical Foundations of Gauge Theories
- The Mathematics of the Bose Gas and its Condensation
- The Structure of Complex Lie Groups (CHAPMAN & HALL/ CRC RESEARCH NOTES IN MATHEMATICS)
- Topological Quantum Field Theory and Four Manifolds (Mathematical Physics Studies) - Jose Labastida, Marcos Marino
- Topology and Geometry for Physicists
- Topology and Geometry in Physics (Lecture Notes in Physics)
- To Quantum Information Theory and Quantum Statistics (Theoretical and Mathematical Physics) - Dénes Petz
- Quantum Magnetism (Lecture Notes in Physics)
- Quarks, Leptons and the Big Bang
- Quaternions, Clifford Algebras and Relativistic Physics - Patrick R. Girard
- Selected Problems in Theoretical Physics
- Statistical Mechanics: From First Principles to Macroscopic Phenomena
- Statistical Physics - Akira Isihara
- Supersymmetric Quantum Cosmology (Cambridge Monographs on Mathematical Physics) - P. D. D’Eath
- Tensor Analysis - L.P. Lebedev, Michael J. Cloud
- Tensors and Manifolds: with Applications to Mechanics and Relativity - Robert H. Wasserman
- The Geometry of Physics: An Introduction - Theodore Frankel
- The Mathematical Foundations of Gauge Theories
- The Mathematics of the Bose Gas and its Condensation
- The Structure of Complex Lie Groups (CHAPMAN & HALL/ CRC RESEARCH NOTES IN MATHEMATICS)
- Topological Quantum Field Theory and Four Manifolds (Mathematical Physics Studies) - Jose Labastida, Marcos Marino
- Topology and Geometry for Physicists
- Topology and Geometry in Physics (Lecture Notes in Physics)
- Topology, Geometry, and Gauge Fields: Interactions (Applied Mathematical Sciences) - Gregory L. Naber
- Waves: A Mathematical Approach to the Common Types of Wave Motion (Longman Mathematical Texts)
- Topology, Geometry, and Gauge Fields: Interactions (Applied Mathematical Sciences) - Gregory L. Naber
- Waves: A Mathematical Approach to the Common Types of Wave Motion (Longman Mathematical Texts)









